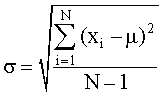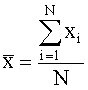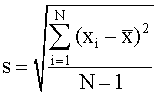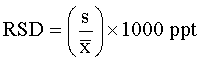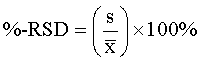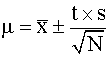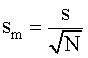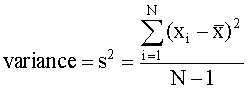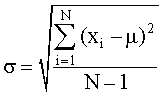Apn setting for du and etisalat uae


ETISALAT

Name : DATA Package
APN: etisalat.ae
Proxy: Not Set
User Name: Not Set
Password: Not Set
Server: Not Set
MMSC: Not Set
MMS Proxy: Not Set
MMS Port Not Set
MCC: 424
MNC: 02
Authentication Type: PAP
APN type: default, supl

* it has separate configuration for its MMS

Name: Etisalat MMS
APN: etisalat
Proxy: Not Set
Port: Not Set
Username: Not Set
Server: Not Set
MMS Proxy: 10.12.0.32
MMS Port: 8080
MCC: 424
MNC: 02
Authentication type: PAP
APN type: MMS
Bearer: Unspecified


DU

Name: du
APN: du
Proxy: Not set
Port: Not set
User Name: Not set
Password: Not Set
Server: Not Set
MMS Proxy: 10.19.18.4
MMS Port: 8080
MCC: 424
MNC: 03
Authentication type: PAP
APN Type: default, mms, supl
Bearer:unspecified

Shape of normal distribution when standard deviation is ZERO

When standard deviation is zero, you will not have a curve with a shape, but just the middle line that represents the mean/median/mode
For any distribution, the smallest possible value for the standard deviation is zero. From the definition of the normal distribution centered at 0, \frac{1}{\sigma \sqrt{\pi}} \exp^{-\frac{x^{2}}{\sigma ^{2}}} , we can't just set \sigma = 0, because we can not divide by zero.

Instead, we should examine what happens as \sigma \to 0. We know that \sigma is fundamentally related to what people interpret as the 'width' of the distribution. So, as \sigma \to 0 know that the 'width' of the distribution will get narrower. The area under the distribution always has to integrate to zero, so the 'height' of the distribution will get taller to compensate for decreasing 'width.'

Taking this to its logic conclusion, we have a distribution function that is zero everywhere except that the center (in the above example, at x=0) and at x=0 is..... well.... that is kind of the rub. Infinity isn't really a number that it makes sense for a function to have as a value. We want to say the distribution has a value of infinity at the point it was originally centered around. This is not strictly correct, but it is correct enough to be the useful way to think about it in applications like physics and signals processing.

A coefficient of variation (CV)

A statistical measure of the dispersion of data points in a data series around the mean. It is calculated as follows:
Coefficient Of Variation (CV)


The coefficient of variation represents the ratio of the standard deviation to the mean, and it is a useful statistic for comparing the degree of variation from one data series to another, even if the means are drastically different from each other.

A coefficient of variation (CV) can be calculated and interpreted in two different settings: analyzing a single variable and interpreting a model.  The standard formulation of the CV, the ratio of the standard deviation to the mean, applies in the single variable setting. In the modeling setting, the CV is calculated as the ratio of the root mean squared error (RMSE) to the mean of the dependent variable. In both settings, the CV is often presented as the given ratio multiplied by 100. The CV for a single variable aims to describe the dispersion of the variable in a way that does not depend on the variable's measurement unit. The higher the CV, the greater the dispersion in the variable. The CV for a model aims to describe the model fit in terms of the relative sizes of the squared residuals and outcome values.  The lower the CV, the smaller the residuals relative to the predicted value.  This is suggestive of a good model fit. 

Advantages

The advantage of the CV is that it is unitless.  This allows CVs to be compared to each other in ways that other measures, like standard deviations or root mean squared residuals, cannot be. 
In the variable CV setting: The standard deviations of two variables, while both measure dispersion in their respective variables, cannot be compared to each other in a meaningful way to determine which variable has greater dispersion because they may vary greatly in their units and the means about which they occur. The standard deviation and mean of a variable are expressed in the same units, so taking the ratio of these two allows the units to cancel.  This ratio can then be compared to other such ratios in a meaningful way: between two variables (that meet the assumptions outlined below), the variable with the smaller CV is less dispersed than the variable with the larger CV.
In the model CV setting: Similarly, the RMSE of two models both measure the magnitude of the residuals, but they cannot be compared to each other in a meaningful way to determine which model provides better predictions of an outcome. The model RMSE and mean of the predicted variable are expressed in the same units, so taking the ratio of these two allows the units to cancel.  This ratio can then be compared to other such ratios in a meaningful way: between two models (where the outcome variable meets the assumptions outlined below), the model with the smaller CV has predicted values that are closer to the actual values.  It is interesting to note the differences between a model's CV and R-squared values.  Both are unitless measures that are indicative of model fit, but they define model fit in two different ways: CV evaluates the relative closeness of the predictions to the actual values while R-squared evaluates how much of the variability in the actual values is explained by the model. 

What is standard deviation (SD)

If data values are all equal to one another, then the standard deviation is zero.
If a high proportion of data points lie near the mean value, then the standard deviation is small. An experiment that yields data with a low standard deviation is said have high precision.
If a high proportion of data points lie far from the mean value, then the standard deviation is large. An experiment that yields data with a high standard deviation is said to have low precision.
The following quantities/equations are quantitative measures of precision.
The equations provide precision measures for a limited number of repetitive measurements, i.e. between 2 and 20. The equation at the end is the true standard deviation for any number of repeat measurements.
The mean or average, 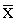x-bar, is calculated from:
mean

Where N is the number of measurements and xi is each individual measurement. 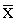x-bar is sometimes called the sample mean to differentiate it from the true orpopulation mean, μ. The formula for μ is the same as above, but N must be at least 20 measurements.
Standard Deviation
The standard deviation, s, is a statistical measure of the precision for a series of repetitive measurements. The advantage of using s to quote uncertainty in a result is that it has the same units as the experimental data. Under a normal distribution, ± one standard deviation encompasses 68% of the measurements and ± two standard deviations encompasses 96% of the measurements. It is calculated from:
standard deviation
Where N is the number of measurements, xi is each individual measurement, and 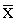x-bar is the mean of all measurements.
The quantity (xi - 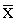x-bar) is called the "residual" or the "deviation from the mean" for each measurement. The quantity (N - 1) is called the "degrees of freedom" for the measurement.
Relative standard Deviation
The relative standard deviation (RSD) is useful for comparing the uncertainty between different measurements of varying absolute magnitude. The RSD is calculated from the standard deviation, s, and is commonly expressed as parts per thousand (ppt) or percentage (%):
The %-RSD is also called the "coefficient of variance" or CV.
Confidence Limits
Confidence limits are another statistical measure of the precision for a series of repetitive measurements. They are calculated from the standard deviation using:
confidence limits
You would say that with some confidence, for example 95%, the true value is between the confidence limits. The t term is taken from a table for the number of degrees of freedom and the degree of confidence desired. t values for finding confidence limits D.F. 90% 95% 99% 16.3112.7163.6622.924.309.9332.353.185.8442.132.784.6052.012.574.0361.942.453.7171.902.373.50151.752.132.95 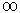infinity1.651.962.58
You might also encounter the term "confidence interval".
The confidence interval is the span between the confidence limits:
confidence interval
Other Measures of Precision
The quantitative measures of precision described above are the most common for reporting analytical results. You might encounter other measures of precisions, and several other quantities are listed here for completeness.
Standard Error
standard error
variance
The advantage of working with variance is that variances from independent sources of variation may be summed to obtain a total variance for a measurement.
All of the equations above are intended to obtain the precision of a relatively small numbers of repeated measurements. For 20 or more measurements you need to use:
The True or Population Standard Deviation
This is given the symbol sigma:
sigma
The equation is:
kishorkc.blogspot.com
Subscribe to: Posts (Atom)